Parte 1: Calculando coordenadas finais possuindo um ponto inicial, a distância e o Azimute ( ângulo)
Contornos de Propagação para Radiodifusão plotados no Google Earth parte 1
.
Parte 1: Calculando coordenadas finais possuindo um ponto inicial, a distância e o Azimute ( ângulo)
Olá esporádicos leitores do RedRails, hoje vamos começar uma serie sobre cálculos de coordenadas, Google Earth e Ruby. Me foi proposto um problema, um engenheiro de telecomunicações tem um grande trabalho na hora de desenvolver seus projetos quanto ao desenho do alcance de uma antena de radiodifusão, pois deve traçar o raio de alcance dessa antena em todas as direções, ou seja, se ele for considerar os 360 graus do circulo e sendo que deve desenhar quatro contornos de alcance teríamos 1440 pontos, isso dá um trabalho considerável.
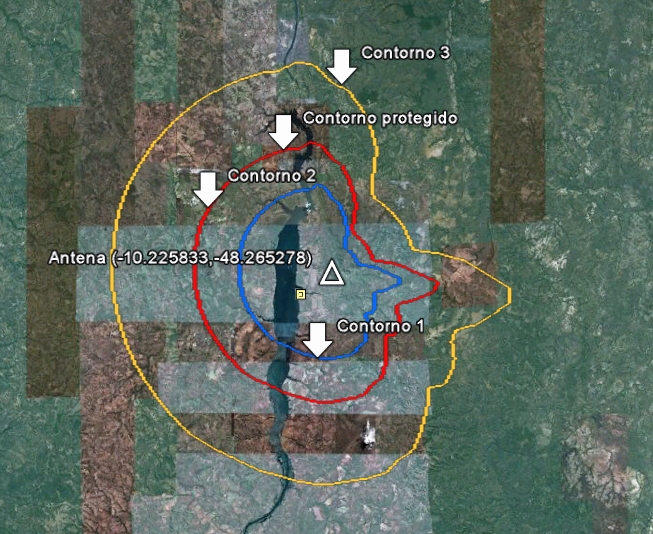
Logo abaixo temos uma amostra do resultado a ser atingido. Temos 3 traçados visíveis, pois o contorno 2 e o contorno protegido são equivalentes. A antena é simbolizada pelo triângulo no centro dos contornos, observem a irregularidade apresentada no lado direito da imagem. É exatamente esse o intuído dessa plotagem demonstrar visualmente o alcance e as possíveis adversidades que seu sinal pode encontrar em nosso exemplo uma cadeia de montanhas está obstruindo o sinal.
Como podemos solucionar esse tipo de problema? Primeiro analisaremos nossas variáveis, conhecemos uma coordenada inicial (onde a torre se encontra, ou um provável local para sua implantação): lat1, lon1. A ANATEL disponibiliza para esse tipo de trabalho as distâncias para até os contornos para cada azimute (grau de inclinação da reta em relação ao norte verdadeiro) que em nosso caso vai ser uma sequencia definida da criação do contorno.
Agora para calcular a coordenada referente a cada dado disponibilizado foi a parte mais trabalhosa, depois de algum tempo de pesquisa conseguimos encontrar uma função matemática que resolveu nosso problema.
A Fórmula Direta de Vincenty (Vincenty ‘Direct’ formula)
Para facilitar o entendimento nosso amigo Chris Veness a converteu em algoritmo:
a, b = major & minor semiaxes of the ellipsoid
f = flattening (a−b)/a
φ1, φ2 = geodetic latitude
s = length of the geodesic
α1, α2 = azimuths of the geodesic (initial/final bearing)tanU1 = (1−f).tanφ1 (U is ‘reduced latitude’)
cosU1 = 1/√(1+tan²U1), sinU1 = tanU1.cosU1 (trig identities; §6)
σ1 = atan2(tanU1, cosα1) (1) sinα = cosU1.sinα1 (2) cos²α = 1 − sin²α (trig identity; §6)
u² = cos²α.(a²−b²)/b²
A = 1+u²/16384.{4096+u².[−768+u².(320−175.u²)]}(3)
B = u²/1024.{256+u².[−128+u².(74−47.u²)]}(4)
σ = s / b.A (1st approximation), σ′ = 2πwhile abs(σ−σ′) > 10-12 { (i.e. 0.06mm)
cos2σm = cos(2.σ1 + σ) (5)
Δσ = B.sinσ.{cos2σm + B/4.[cosσ.(−1 + 2.cos²2σm) − B/6.cos2σm.(−3 + 4.sin²σ).(−3 + 4.cos²2σm)]} (6) σ′ = σ σ = s / b.A + Δσ (7)
}φ2 = atan2(sinU1.cosσ + cosU1.sinσ.cosα1, (1−f).√[sin²α + (sinU1.sinσ − cosU1.cosσ.cosα1)²]) (8)
λ = atan2(sinσ.sinα1, cosU1.cosσ − sinU1.sinσ.cosα1) (9)C = f/16.cos²α.[4+f.(4−3.cos²α)] (10)
L = λ − (1−C).f.sinα.{σ+C.sinσ.[cos2σm + C.cosσ.(−1 + 2.cos²2σm)]} (difference in longitude) (11) α2 = atan2(sinα, −sinU1.sinσ + cosU1.cosσ.cosα1) (reverse azimuth) (12)
p2 = (φ2, λ1+L)
E finalmente nosso código em Ruby.
[ruby]
<pre>
<div id="LC4">class Vincent</div>
<div id="LC5"> def initialize(lat1,lon1)</div>
<div id="LC6"> #Origem e Destino</div>
<div id="LC7"> @lat1 = lat1</div>
<div id="LC8"> @lon1=lon1</div>
<div id="LC9"></div>
<div id="LC10"> #---- Dados do Elipsóide de Revolução --------------------------------------</div>
<div id="LC11"> #http://pt.wikipedia.org/wiki/Figura_da_Terra</div>
<div id="LC12"> @a = 6378137 # Maior semi-eixo da Elipsóide Terrestre - WGS66 (1966)[EUA/DoD]</div>
<div id="LC13"> @b = 6356752.3142 # Maior semi-eixo da Elipsóide Terrestre - WGS66 (1966)[EUA/DoD]</div>
<div id="LC14"> @f = 1/298.257223563 # Achatamento inverso - WGS66 (1966)[EUA/DoD]</div>
<div id="LC15"> end</div>
<div id="LC17"> #------------ ADDONS ------------------------</div>
<div id="LC18"> def todeg(num)</div>
<div id="LC19"> num*57.29578</div>
<div id="LC20"> end</div>
<div id="LC22"> def torad(angle)</div>
<div id="LC23"> angle/57.29578</div>
<div id="LC24"> end</div>
<div id="LC26"> # - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -</div>
<div id="LC27"> #</div>
<div id="LC28"> #{} Calculate destination point given start point lat/long (numeric degrees),</div>
<div id="LC29"> # bearing (numeric degrees) & distance (in m).</div>
<div id="LC30"> #</div>
<div id="LC31"> # from: Vincenty direct formula - T Vincenty, "Direct and Inverse Solutions of Geodesics on the</div>
<div id="LC32"> # Ellipsoid with application of nested equations", Survey Review, vol XXII no 176, 1975</div>
<div id="LC33"> # http://www.ngs.noaa.gov/PUBS_LIB/inverse.pdf</div>
<div id="LC34"> #</div>
<div id="LC35"> def calculate(az, dist)</div>
<div id="LC36"> s = dist</div>
<div id="LC37"> alpha1 = torad(az)</div>
<div id="LC38"> cos_alpha1 = Math.cos(alpha1)</div>
<div id="LC39"> sin_alpha1 = Math.sin(alpha1)</div>
<div id="LC41"> tan_u1 = (1-@f) * Math.tan(torad(@lat1))</div>
<div id="LC42"> cos_u1 = 1 / Math.sqrt((1 + tan_u1*tan_u1))</div>
<div id="LC43"> sin_u1 = tan_u1*cos_u1</div>
<div id="LC44"> sigma1 = Math.atan2(tan_u1, cos_alpha1)</div>
<div id="LC45"> sin_alpha = cos_u1 * sin_alpha1;</div>
<div id="LC46"> cos_sq_alpha = 1 - sin_alpha*sin_alpha;</div>
<div id="LC47"> u_sq = cos_sq_alpha * (@a*@a - @b*@b) / (@b*@b)</div>
<div id="LC48"> an = 1 + u_sq/16384*(4096+u_sq*(-768+u_sq*(320-175*u_sq)));</div>
<div id="LC49"> bn = u_sq/1024 * (256+u_sq*(-128+u_sq*(74-47*u_sq)));</div>
<div id="LC51"> sigma = (s / (@b*an))</div>
<div id="LC52"> sigma_p = (2*Math::PI)</div>
<div id="LC53"> while true</div>
<div id="LC54"> cos2_sigma_m = Math.cos(2*sigma1 + sigma);</div>
<div id="LC55"> sin_sigma = Math.sin(sigma)</div>
<div id="LC56"> cos_sigma = Math.cos(sigma)</div>
<div id="LC57"> delta_sigma = bn*sin_sigma*(cos2_sigma_m+bn/4*(cos_sigma*(-1+2*cos2_sigma_m*cos2_sigma_m)-</div>
<div id="LC58"> bn/6*cos2_sigma_m*(-3+4*sin_sigma*sin_sigma)*(-3+4*cos2_sigma_m*cos2_sigma_m)));</div>
<div id="LC59"> sigma_p = sigma;</div>
<div id="LC60"> sigma = s / (@b*an) + delta_sigma;</div>
<div id="LC61"> break if ((sigma.abs-sigma_p) > 1.0e-012) or sigma.abs==sigma_p</div>
<div id="LC62"> end</div>
<div id="LC64"> tmp = sin_u1*sin_sigma - cos_u1*cos_sigma*cos_alpha1;</div>
<div id="LC65"> lat2 = Math.atan2(sin_u1*cos_sigma + cos_u1*sin_sigma*cos_alpha1,</div>
<div id="LC66"> (1-@f)*Math.sqrt(sin_alpha*sin_alpha + tmp*tmp));</div>
<div id="LC67"> lambda = Math.atan2(sin_sigma*sin_alpha1, cos_u1*cos_sigma - sin_u1*sin_sigma*cos_alpha1);</div>
<div id="LC68"> cn = @f/16*cos_sq_alpha*(4+@f*(4-3*cos_sq_alpha));</div>
<div id="LC69"> ln = lambda - (1-cn) * @f * sin_alpha *</div>
<div id="LC70"> (sigma + cn*sin_sigma*(cos2_sigma_m+cn*cos_sigma*(-1+2*cos2_sigma_m*cos2_sigma_m)));</div>
<div id="LC72"> rev_az = Math.atan2(sin_alpha, -tmp);</div>
<div id="LC74"> {:lat=>todeg(lat2),:lon=> @lon1+todeg(ln),:rev_az=>rev_az}</div>
<div id="LC75">#C: -9.740848496159662,-48.04187046994603</div>
<div id="LC77"> end</div>
<div id="LC80">end</div></pre>
[/ruby]
Logo mais teremos mais post sobre o assunto.
o Projeto já implementado vocês podem conferir em meu Github

Agradecimentos a Eng. Antonio Ernani por toda colaboração e para geração dos poligonos vejam o próximo post (http://www.redrails.com.br/2010/11/desenho-de-poligonos-no-google-earth-usando-ruby/)